剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

题目描述：

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例：

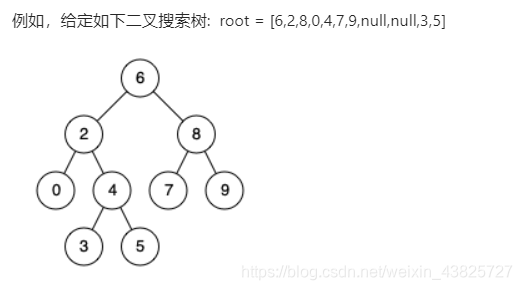
在这里插入图片描述

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身

思路：

这道题和二叉树的最近公共祖先的唯一差别就是本题的树是二叉搜索树（BST），也就暗示我们需要使用BST的特性。
由于lowestCommonAncestor(root, p, q)的功能是找出以root为根节点的两个节点p和q的最近公共祖先。 我们考虑：

如果p和q分别在root两侧，那么root就是最近公共祖先。我们使用(root.val - p.val) * (root.val - q.val) <= 0来判断即可。
否则的话（p和q在某一颗子树上），我们继续判断p是否在左子树。如果在（p在q一定也在），我们返回递归去左子树找。如果不在我们返回递归去右子树找

代码：

1
2
3
4
5
6
7
8
9
var lowestCommonAncestor = function(root, p, q) {
    if ((root.val - p.val) * (root.val - q.val) <= 0) {
        return root
    }else if (p.val < root.val) {
        return lowestCommonAncestor(root.left, p, q)
    }else{
        return lowestCommonAncestor(root.right, p, q)
    }
};