剑指 Offer 47. 礼物的最大价值

题目描述：

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例：

输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

思路：

简单的动态规划。类似于青蛙跳台阶，分情况分析明确之后就很容易做了。
以测试用例为例，棋盘大小m=3,n=3,即grid;如下图: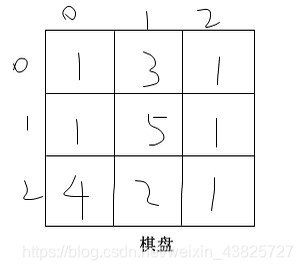
在这里插入图片描述
第一步：构建一个与棋盘相当的二维数组，代表移动到每个棋盘格上时此处的最大礼物价值，即value；如下图: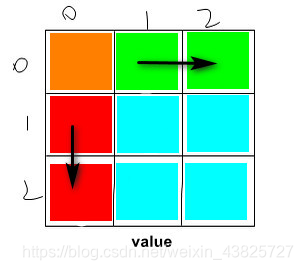
在这里插入图片描述
由上图可得，价值棋盘共有4中情况：

  1. 左上角，即value[0][0] == grid[0][0]；因为这是开始端
  2. 当m = 0 , 即第一行value[0][n] ; 只能从右侧移动过来，所以公示为: value[0][j] = value[0][j
    • 1] + grid[0][j] ; j代表当前列
  3. 当n = 0，即第一列value[m][0]；只能从上面移动过来；公示为： value[i][0] = value[i - 1][0]
    • grid[i][0]; i代表当前行
  4. 最后一种情况，即蓝色部分，此时就要选择从右侧或者上侧过来的最大值，公示为：value[i][j] = Math.max((value[i
    • 1][j] + grid[i][j]) , (value[i][j - 1] + grid[i][j]));

所以全部情况弄清楚之后就可以得到一个value二维数组，最后返回右下角的值即

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var maxValue = function(grid) {
    let inputArr = grid;
    let value = [];
    let m = 0;
    let n = 0;
    //inputArr = JSON.parse(inputArr);
	m = inputArr.length;
	n = inputArr[0].length;
	for(let i = 0 ; i < m ; i ++){
		value[i] = [];
		for(let j = 0 ; j < n ; j ++){
			//当左上角
			if(i == 0 && j == 0){
				value[i][j] = inputArr[i][j];
			}else if(i == 0){
				//i代表行，行为第一行时，只能从右边过来
				value[i][j] = value[i][j - 1] + inputArr[i][j];
			}else if(j == 0){
				//j代表列，第一列时只能从上面下来
				value[i][j] = value[i - 1][j] + inputArr[i][j];
			}else{
				//若为其余情况，则取上面下来和右边过来的最大值作为结果
				value[i][j] = Math.max((value[i - 1][j] + inputArr[i][j]) , (value[i][j - 1] + inputArr[i][j]));
			}			
		}
	}
    return value[m - 1][n - 1];
};